Mathematics: the Language of Numbers
by Cathie Maglio, Blended Learning SPECIALIST
The other day I saw an entry on a social media site in which two students were talking about their classes.
One exchange went like this:
This isn’t the first time I’ve heard that math seems like a foreign language to some people. It’s true that math is its own language. Like any language, you learn it by studying its vocabulary, grammar, syntax and literature. Once you learn it, it isn’t foreign anymore.
Peter Hilton of SUNY Binghamton writes in his book Mathematics: From the Birth of Numbers that, “the most common fallacy is to confuse mathematics with elementary arithmetic and to think that progress is measured by performing ever more complicated calculations with speed, dexterity, and accuracy.” I agree that mathematics is so much more than calculation. To a mathematics speaker, the language of math is as much an expression of the human spirit as literature, music or painting.
I recently took a class called Technology and Language Arts that included mathematics in the definition of language. The syllabus defined language arts as: “the cognitive and social development that leads to the acquisition of the skills necessary to communicate and articulate ideas, feelings, and information. It is the way we express ourselves, the way we process information, and the way we apply the information we have received.”
How does this definition apply to mathematics? Breaking the definition into two parts shows how mathematics belongs in language arts.
Part I: In the early years, teaching math is simply teaching arithmetic. This fulfills part one of the definition: “Students learn the skills necessary to communicate ideas, feelings and information.” In arithmetic, students learn about numbers: the words one two three, the symbols 1 2 3, and the quantities represented by the numbers. The association between the word, the symbol, and the quantity is committed to memory and used to express ideas. When the number 5 is seen, the mind reads five and visualizes or thinks of the quantity of five objects. The number is a symbol for the word which is a symbol for the object. Numerals are used as a shorthand for numbers since it is easier than writing the words, especially with large numbers such as “one million, six hundred forty-five thousand, and three hundred two” (1,645,302). Students learn to write numbers using both words and numerals.
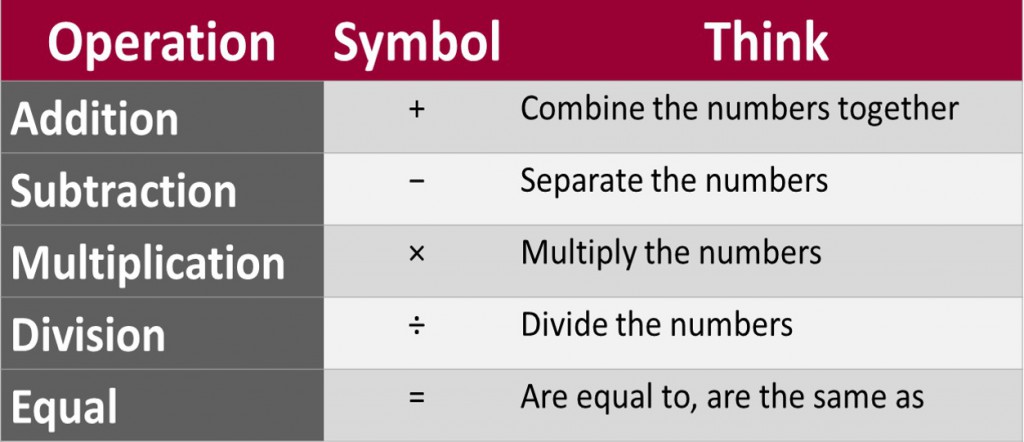
Once number association is learned, students move on to the computational skills of arithmetic, learning the operations we use to manipulate numbers. The four basic operations– addition, subtraction, multiplication, and division– are the foundation of all mathematics. Again symbols are used to represent words which represent computational actions. The mind sees a symbol, thinks a word and understands an action.
To practice these skills, manipulatives may be used to help students understand each operation and how they are related, i.e. addition is the opposite of subtraction and multiplication is the opposite of division.
Part II: Once having learned these concepts and skills, students move to the second part of the definition: “To express ourselves, to process the information, and to apply the information we have learned.” This describes the introduction of word problems and problem solving skills. In a word problem, the student reads the words, interprets the information and translates it into a mathematical model. All the information needed to solve the problem is given. Difficulty can arise in gathering and processing the information to write a mathematical model that will lead to a solution to the problem. It is helpful to write a verbal model of the problem before writing the mathematical model.
All word problems have the same basic components: a problem that needs to be solved, the information that defines the problem, the operation(s) to be used, and a conclusion derived from the results of the operations. Every word problem can be dissected into these components. Here is an example:

Not all word problem are this simple; but even the most difficult problem can be dissected into its components and a verbal model can be written to make solving the problem easier by giving it structure and sequence. One of the most difficult tasks in solving a word problem is determining the operation to be used and writing the mathematical statement that shows how the information is related.
Yes, math is a language. But it is no more foreign than the language of music. Once the melody, harmony and rhythm of math are learned, any problem can be solved. Just like music, mathematics is a language that expresses the human spirit. With practice, anyone can learn to speak it. With more practice, you can learn to sing it.